Biases (Verzerrungen) sind eine Art von Parametern in neuronalen Netzwerken, die dazu dienen, die Aktivierung von Neuronen zu steuern. Jedes Neuron hat einen Bias-Wert, der eine Konstante ist und zu der gewichteten Summe der Eingaben addiert wird, bevor sie durch eine Aktivierungsfunktion geleitet werden. Der Bias ermöglicht es einem neuronalen Netzwerk, auch ohne Eingaben zu feuern und trägt zur Flexibilität und Anpassungsfähigkeit des Modells bei.

Weights (Gewichte) sind Parameter, die in neuronalen Netzwerken verwendet werden, um die Stärke der Verbindungen zwischen Neuronen zu steuern. Jede Verbindung zwischen zwei Neuronen hat ein Gewicht, das die Bedeutung oder den Einfluss dieser Verbindung auf die Ausgabe des nächsten Neurons angibt. Während des Trainings eines neuronalen Netzwerks werden die Gewichte so angepasst, dass das Netzwerk die gewünschten Ausgaben für gegebene Eingaben erzeugt. Die Gewichte bestimmen im Wesentlichen, wie viel Einfluss ein Neuron auf das nächste hat und spielen eine entscheidende Rolle bei der Berechnung der Aktivierung und der Ausgabe des Netzwerks.

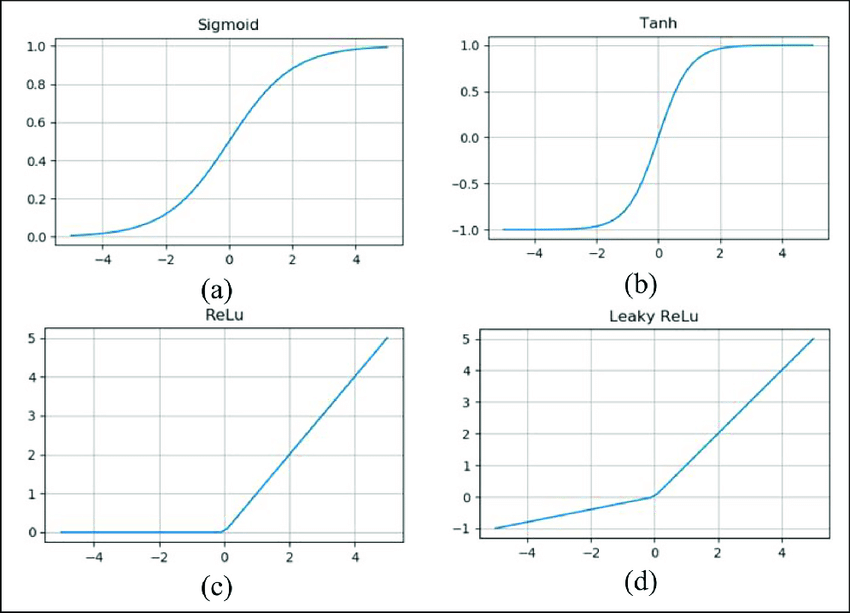
Aktivierungsfunktionen werden in neuronalen Netzen verwendet, um die Ausgabe eines Neurons zu berechnen. Sie fügen nichtlineare Eigenschaften in das Modell ein und ermöglichen es dem Netzwerk, komplexe Muster und Zusammenhänge in den Daten zu erfassen. Beispiele für Aktivierungsfunktionen sind die Sigmoid-Funktion, die ReLU (Rectified Linear Unit) und die tanh-Funktion.

Die Sigmoid-Funktion, auch logistische Funktion genannt, ist eine Aktivierungsfunktion, die oft in neuronalen Netzwerken verwendet wird, insbesondere in früheren Modellen. Sie hat die Form f(x) = 1 / (1 + e^(-x)) und gibt Werte zwischen 0 und 1 aus. Sie wird häufig in binären Klassifikationsaufgaben verwendet, da sie eine Wahrscheinlichkeitsinterpretation ermöglicht.

#include <stdio.h>
#include <math.h>
 
float sigmoid(float x) {
    return 1 / (1 + exp(-x));
}
 
int main() {
    float input = 0.8;
    float output = sigmoid(input);
    printf("Sigmoid(%f) = %f\n", input, output);
    return 0;
}

Rectified Linear Unit (ReLU): Die ReLU-Funktion ist eine weit verbreitete Aktivierungsfunktion, die für viele Anwendungen gute Ergebnisse liefert. Sie ist definiert als f(x) = max(0, x), d.h. sie gibt die Eingabe unverändert zurück, wenn sie positiv ist, andernfalls gibt sie 0 zurück. Die ReLU-Funktion ist einfach zu berechnen und kann zur Lösung des Vanishing-Gradient-Problems beitragen.

#include <stdio.h>
 
float relu(float x) {
    return (x > 0) ? x : 0;
}
 
int main() {
    float input = 2.5;
    float output = relu(input);
    printf("ReLU(%f) = %f\n", input, output);
    return 0;
}

Leaky ReLU: Die Leaky ReLU-Funktion ist eine Variante der ReLU-Funktion, bei der eine kleine, konstante Steigung für negative Eingaben eingeführt wird, um das Problem der „tote Neuronen“ zu mildern. Es wird definiert als f(x) = max(αx, x), wobei α eine kleine positive Konstante ist.

#include <stdio.h>
 
float leaky_relu(float x, float alpha) {
    return (x > 0) ? x : alpha * x;
}
 
int main() {
    float input = -1.8;
    float alpha = 0.01;
    float output = leaky_relu(input, alpha);
    printf("Leaky ReLU(%f, %f) = %f\n", input, alpha, output);
    return 0;
}

Exponential Linear Unit (ELU): Die ELU-Funktion ist eine weitere Aktivierungsfunktion, die die Vorteile der ReLU-Funktion beibehält und auch für negative Eingaben einen sanften Übergang ermöglicht. Sie ist definiert als f(x) = x, wenn x > 0 und f(x) = α(e^x - 1), wenn x ⇐ 0, wobei α eine positive Konstante ist.

#include <stdio.h>
#include <math.h>
 
float elu(float x, float alpha) {
    return (x > 0) ? x : alpha * (exp(x) - 1);
}
 
int main() {
    float input = -2.0;
    float alpha = 0.1;
    float output = elu(input, alpha);
    printf("ELU(%f, %f) = %f\n", input, alpha, output);
    return 0;
}

Hyperbolic Tangent (Tanh): Die Tangens Hyperbolicus-Funktion ist eine S-förmige Aktivierungsfunktion, die Werte zwischen -1 und 1 ausgibt. Sie ist definiert als f(x) = (e^x - e^(-x)) / (e^x + e^(-x)). Die Tanh-Funktion ist symmetrisch um den Ursprung und erzeugt sowohl positive als auch negative Aktivierungen.

#include <stdio.h>
#include <math.h>
 
float tanh_activation(float x) {
    return tanh(x);
}
 
int main() {
    float input = 1.2;
    float output = tanh_activation(input);
    printf("tanh(%f) = %f\n", input, output);
    return 0;
}

Die Maxout-Funktion verwendet einen Pool von Neuronen und gibt das Maximum der Aktivierungen in diesem Pool aus. Es findet eine „maximale Aktivierung“ statt, indem die Eingaben zu den Neuronen in mehrere Gruppen aufgeteilt werden und das Maximum der Aktivierungen ausgewählt wird.

Mathematisch ausgedrückt kann die Maxout-Funktion als f(x) = max(w1x + b1, w2x + b2) dargestellt werden, wobei w1 und w2 die Gewichte, b1 und b2 die Bias-Termine sind.

#include <math.h>
 
double maxout(double x1, double x2) {
    return fmax(x1, x2);
}
 
int main() {
    double input1 = 2.5;
    double input2 = -1.8;
 
    double result = maxout(input1, input2);
 
    printf("maxout(%f, %f) = %f\n", input1, input2, result);
 
    return 0;
}

Verlustfunktionen messen den Fehler oder die Diskrepanz (Gradient) zwischen den Vorhersagen eines neuronalen Netzwerks und den tatsächlichen Zielwerten. Sie dienen als Grundlage für das Training des Netzwerks, da das Ziel darin besteht, die Verlustfunktion zu minimieren. Beispiele für Verlustfunktionen sind der quadratische Fehler, der Kreuzentropie-Fehler und der Huber-Verlust.

Optimierungsalgorithmen werden verwendet, um die Gewichte und Biases eines neuronalen Netzwerks anzupassen, um die Verlustfunktion zu minimieren. Diese Algorithmen suchen nach dem globalen Minimum der Verlustfunktion und passen die Parameter schrittweise an, um dieses Minimum zu erreichen. Beispiele für Optimierungsalgorithmen sind der Gradientenabstieg, der stochastische Gradientenabstieg (SGD) und der Adam-Optimierer.

Overfitting tritt auf, wenn ein Modell zu stark an die Trainingsdaten angepasst ist und die Fähigkeit verliert, auf neuen Daten gut zu verallgemeinern.

Underfitting hingegen tritt auf, wenn ein Modell zu einfach ist und nicht in der Lage ist, die zugrunde liegenden Muster der Daten zu erfassen. Das Finden des richtigen Gleichgewichts zwischen Overfitting und Underfitting ist ein wichtiges Ziel beim Trainieren von neuronalen Netzen.

Die Batch-Größe bezieht sich auf die Anzahl der Trainingsbeispiele, die in einem Durchlauf des Trainingsalgorithmus verwendet werden. Eine größere Batch-Größe kann zu einer effizienteren Berechnung führen, während eine kleinere Batch-Größe dazu beitragen kann, das Modell besser zu generalisieren.

Die Lernrate bestimmt, wie stark die Gewichte und Biases bei jedem Aktualisierungsschritt angepasst werden. Eine zu hohe Lernrate kann zu instabilen Modellen führen, während eine zu niedrige Lernrate das Konvergenzverhalten des Netzwerks verlangsamen kann.

Beim Netzwerkdurchlauf, der den Fluss der Daten und Berechnungen in einem neuronalen Netzwerk beschreibt, gibt es verschiedene Konzepte.

Der Vorwärtsdurchlauf ist der erste Schritt des Netzwerkdurchlaufs. Dabei werden die Eingabedaten durch das Netzwerk geleitet, indem Berechnungen schichtweise durchgeführt werden. Jedes Neuron berechnet die gewichtete Summe seiner Eingaben, fügt den Bias-Wert hinzu und leitet das Ergebnis durch eine Aktivierungsfunktion, um die Aktivierung des Neurons zu bestimmen. Der Vorwärtsdurchlauf bewegt sich von der Eingabeschicht bis zur Ausgabeschicht und erzeugt eine Vorhersage oder eine Ausgabe des Netzwerks.

Der Rückwärtsdurchlauf ist der Schritt, der nach dem Vorwärtsdurchlauf erfolgt und beim Training eines neuronalen Netzwerks verwendet wird. Nachdem die Vorhersage oder Ausgabe generiert wurde, wird der Rückwärtsdurchlauf verwendet, um den Fehler oder die Diskrepanz zwischen den Vorhersagen des Netzwerks und den tatsächlichen Zielwerten zu berechnen. Dieser Fehler wird dann verwendet, um den Gradienten der Verlustfunktion bezüglich der Gewichte und Biases des Netzwerks zu berechnen. Der Gradient gibt die Richtung an, in der die Gewichte und Biases angepasst werden müssen, um den Verlust zu minimieren.

Die Verlustfunktion misst den Fehler oder die Diskrepanz zwischen den Vorhersagen des Netzwerks und den tatsächlichen Zielwerten. Sie wird während des Rückwärtsdurchlaufs verwendet, um den Fehler zu quantifizieren und den Gradienten der Verlustfunktion zu berechnen. Beispiele für Verlustfunktionen sind der mittlere quadratische Fehler (Mean Squared Error, MSE) und die Kreuzentropie.

Im Rückwärtsdurchlauf wird der Gradient der Verlustfunktion bezüglich der Gewichte und Biases des Netzwerks berechnet. Dieser Gradient gibt die Richtung an, in der die Gewichte und Biases angepasst werden müssen, um den Verlust zu minimieren. Die Gradientenberechnung erfolgt durch Anwendung der Kettenregel der Ableitung auf die Berechnungen im Netzwerk.

Nachdem der Gradient berechnet wurde, werden die Gewichte und Biases im Netzwerk mithilfe eines Optimierungsalgorithmus aktualisiert. Der am häufigsten verwendete Algorithmus ist der Gradientenabstieg (Gradient Descent), bei dem die Gewichte und Biases in Richtung des negativen Gradients angepasst werden. Andere Optimierungsalgorithmen wie Adam, RMSprop und AdaGrad können ebenfalls verwendet werden.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
 
#define INPUT_SIZE 8
#define OUTPUT_SIZE 1
#define HIDDEN_SIZE 10
#define LEARNING_RATE 0.1
#define MAX_ITERATIONS 10000
 
double sigmoid(double x) {
    return 1.0 / (1.0 + exp(-x));
}
 
void train(double inputs[][INPUT_SIZE], double outputs[], int num_samples, double hidden_weights[][INPUT_SIZE], double output_weights[][HIDDEN_SIZE], double hidden_bias[], double output_bias[]) {
    double hidden_layer[HIDDEN_SIZE];
    double output_layer[OUTPUT_SIZE];
 
    // Zufällige Initialisierung der Gewichte und Biases
    for (int i = 0; i < HIDDEN_SIZE; i++) {
        hidden_bias[i] = ((double)rand() / RAND_MAX) * 2 - 1;
        for (int j = 0; j < INPUT_SIZE; j++) {
            hidden_weights[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
        }
    }
 
    for (int i = 0; i < OUTPUT_SIZE; i++) {
        output_bias[i] = ((double)rand() / RAND_MAX) * 2 - 1;
        for (int j = 0; j < HIDDEN_SIZE; j++) {
            output_weights[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
        }
    }
 
    // Trainingsschleife
    for (int iteration = 0; iteration < MAX_ITERATIONS; iteration++) {
        double total_error = 0.0;
 
        // Durchlaufen der Trainingsdaten
        for (int sample = 0; sample < num_samples; sample++) {
            // Vorwärtsdurchgang
            for (int i = 0; i < HIDDEN_SIZE; i++) {
                double sum = hidden_bias[i];
                for (int j = 0; j < INPUT_SIZE; j++) {
                    sum += hidden_weights[i][j] * inputs[sample][j];
                }
                hidden_layer[i] = sigmoid(sum);
            }
 
            for (int i = 0; i < OUTPUT_SIZE; i++) {
                double sum = output_bias[i];
                for (int j = 0; j < HIDDEN_SIZE; j++) {
                    sum += output_weights[i][j] * hidden_layer[j];
                }
                output_layer[i] = sigmoid(sum);
            }
 
            // Berechnung des Fehlers
            double error = outputs[sample] - output_layer[0];
            total_error += fabs(error);
 
            // Rückwärtsdurchgang
            double output_delta = error * output_layer[0] * (1.0 - output_layer[0]);
 
            for (int i = 0; i < HIDDEN_SIZE; i++) {
                double hidden_delta = hidden_layer[i] * (1.0 - hidden_layer[i]) * output_delta * output_weights[0][i];
 
                for (int j = 0; j < INPUT_SIZE; j++) {
                    hidden_weights[i][j] += LEARNING_RATE * hidden_delta * inputs[sample][j];
                }
                hidden_bias[i] += LEARNING_RATE * hidden_delta;
            }
 
            for (int i = 0; i < OUTPUT_SIZE; i++) {
                for (int j = 0; j < HIDDEN_SIZE; j++) {
                    output_weights[i][j] += LEARNING_RATE * output_delta * hidden_layer[j];
                }
                output_bias[i] += LEARNING_RATE * output_delta;
            }
        }
 
        // Ausgabe des aktuellen Fehlers
        printf("Iteration: %d, Error: %f\n", iteration, total_error);
 
        // Abbruch, wenn der Fehler klein genug ist
        if (total_error < 0.01) {
            break;
        }
    }
}
 
double predict(double inputs[], double hidden_weights[][INPUT_SIZE], double output_weights[][HIDDEN_SIZE], double hidden_bias[], double output_bias[]) {
    double hidden_layer[HIDDEN_SIZE];
    double output_layer[OUTPUT_SIZE];
 
    // Vorwärtsdurchgang
    for (int i = 0; i < HIDDEN_SIZE; i++) {
        double sum = hidden_bias[i];
        for (int j = 0; j < INPUT_SIZE; j++) {
            sum += hidden_weights[i][j] * inputs[j];
        }
        hidden_layer[i] = sigmoid(sum);
    }
 
    for (int i = 0; i < OUTPUT_SIZE; i++) {
        double sum = output_bias[i];
        for (int j = 0; j < HIDDEN_SIZE; j++) {
            sum += output_weights[i][j] * hidden_layer[j];
        }
        output_layer[i] = sigmoid(sum);
    }
 
    return output_layer[0];
}
 
int main() {
    double inputs[][INPUT_SIZE] = {
        {1, 0, 1, 0, 1, 0, 1, 0},
        {0, 1, 0, 1, 0, 1, 0, 1},
        {1, 0, 1, 1, 1, 0, 1, 0},
        {1, 1, 1, 1, 0, 0, 0, 0},
        {0, 0, 0, 0, 1, 1, 1, 1}
    };
    double outputs[] = {0, 0, 0.7, 1, 1};
    int num_samples = 5;
 
    /* Das sind die Modelldaten */
    double hidden_weights[HIDDEN_SIZE][INPUT_SIZE];
    double output_weights[OUTPUT_SIZE][HIDDEN_SIZE];
    double hidden_bias[HIDDEN_SIZE];
    double output_bias[OUTPUT_SIZE];
 
    train(inputs, outputs, num_samples, hidden_weights, output_weights, hidden_bias, output_bias);
 
    // Beispiel für die Vorhersage mit neuen Daten
    double new_inputs[INPUT_SIZE] = {1, 0, 1, 0, 1, 0, 1, 0};
    double prediction = predict(new_inputs, hidden_weights, output_weights, hidden_bias, output_bias);
 
    printf("Prediction: %f\n", prediction);
 
    return 0;
}

Die Funktion train führt das Training des neuronalen Netzwerks durch. Sie erhält die Trainingsdaten „inputs“ als zweidimensionales Array das die Eingabewerte für jedes Trainingsbeispiel enthält, und „outputs“ als Array das die Bewertung für jedes Trainingsbeispiel enthält. „num_samples“ gibt die Anzahl der Trainingsbeispiele an. Die Funktion aktualisiert die Gewichte und Biases des Netzwerks basierend auf den bisherigen Trainingsdaten.

In der train-Funktion werden zunächst die Gewichte und Biases zufällig im Bereich von -1 bis 1 und die Biases im Bereich von -1 bis 1 gewählt.

Die Funktion verwendet eine Trainingsschleife, in jeder Iteration wird der Fehler für jedes Trainingsbeispiel berechnet und die Gewichte und Biases entsprechend angepasst.

Der Fehler wird durch den Vergleich des erwarteten Ausgabewerts mit dem tatsächlichen Ausgabewert berechnet. Der Fehler wird aufaddiert, um den gesamten Fehler für die aktuelle Iteration zu erhalten.

Nachdem alle Trainingsbeispiele verarbeitet wurden, wird der aktuelle Fehler ausgegeben.

Die Funktion predict führt die Vorhersage für neue Daten durch. Sie erhält die Eingabewerte inputs und die trainierten Gewichte und Biases des Netzwerks. Die Funktion berechnet die Ausgabewerte des Netzwerks für die gegebenen Eingabewerte und gibt den Vorhersagewert zurück.

#include <iostream>
#include <cmath>
#include <vector>
 
class NeuralNetwork {
private:
    int inputSize;
    int outputSize;
    int hiddenSize;
    double learningRate;
    int maxIterations;
 
    std::vector<std::vector<double>> hiddenWeights;
    std::vector<std::vector<double>> outputWeights;
    std::vector<double> hiddenBias;
    std::vector<double> outputBias;
 
public:
    NeuralNetwork(int inputSize, int outputSize, int hiddenSize, double learningRate, int maxIterations) {
        this->inputSize = inputSize;
        this->outputSize = outputSize;
        this->hiddenSize = hiddenSize;
        this->learningRate = learningRate;
        this->maxIterations = maxIterations;
 
        hiddenWeights.resize(hiddenSize, std::vector<double>(inputSize));
        outputWeights.resize(outputSize, std::vector<double>(hiddenSize));
        hiddenBias.resize(hiddenSize);
        outputBias.resize(outputSize);
    }
 
    double sigmoid(double x) {
        return 1.0 / (1.0 + std::exp(-x));
    }
 
    void train(std::vector<std::vector<double>>& inputs, std::vector<double>& outputs) {
        int numSamples = inputs.size();
        std::vector<double> hiddenLayer(hiddenSize);
        std::vector<double> outputLayer(outputSize);
 
        // Zufällige Initialisierung der Gewichte und Biases
        for (int i = 0; i < hiddenSize; i++) {
            hiddenBias[i] = ((double)rand() / RAND_MAX) * 2 - 1;
            for (int j = 0; j < inputSize; j++) {
                hiddenWeights[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
            }
        }
 
        for (int i = 0; i < outputSize; i++) {
            outputBias[i] = ((double)rand() / RAND_MAX) * 2 - 1;
            for (int j = 0; j < hiddenSize; j++) {
                outputWeights[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
            }
        }
 
        // Trainingsschleife
        for (int iteration = 0; iteration < maxIterations; iteration++) {
            double totalError = 0.0;
 
            // Durchlaufen der Trainingsdaten
            for (int sample = 0; sample < numSamples; sample++) {
                // Vorwärtsdurchgang
                for (int i = 0; i < hiddenSize; i++) {
                    double sum = hiddenBias[i];
                    for (int j = 0; j < inputSize; j++) {
                        sum += hiddenWeights[i][j] * inputs[sample][j];
                    }
                    hiddenLayer[i] = sigmoid(sum);
                }
 
                for (int i = 0; i < outputSize; i++) {
                    double sum = outputBias[i];
                    for (int j = 0; j < hiddenSize; j++) {
                        sum += outputWeights[i][j] * hiddenLayer[j];
                    }
                    outputLayer[i] = sigmoid(sum);
                }
 
                // Berechnung des Fehlers
                double error = outputs[sample] - outputLayer[0];
                totalError += std::fabs(error);
 
                // Rückwärtsdurchgang
                double outputDelta = error * outputLayer[0] * (1.0 - outputLayer[0]);
 
                for (int i = 0; i < hiddenSize; i++) {
                    double hiddenDelta = hiddenLayer[i] * (1.0 - hiddenLayer[i]) * outputDelta * outputWeights[0][i];
 
                    for (int j = 0; j < inputSize; j++) {
                        hiddenWeights[i][j] += learningRate * hiddenDelta * inputs[sample][j];
                    }
                    hiddenBias[i] += learningRate * hiddenDelta;
                }
 
                for (int i = 0; i < outputSize; i++) {
                    for (int j = 0; j < hiddenSize; j++) {
                        outputWeights[i][j] += learningRate * outputDelta * hiddenLayer[j];
                    }
                    outputBias[i] += learningRate * outputDelta;
                }
            }
 
            // Ausgabe des aktuellen Fehlers
            std::cout << "Iteration: " << iteration << ", Error: " << totalError << std::endl;
 
            // Abbruch, wenn der Fehler klein genug ist
            if (totalError < 0.01) {
                break;
            }
        }
    }
 
    double predict(std::vector<double>& inputs) {
        std::vector<double> hiddenLayer(hiddenSize);
        std::vector<double> outputLayer(outputSize);
 
        // Vorwärtsdurchgang
        for (int i = 0; i < hiddenSize; i++) {
            double sum = hiddenBias[i];
            for (int j = 0; j < inputSize; j++) {
                sum += hiddenWeights[i][j] * inputs[j];
            }
            hiddenLayer[i] = sigmoid(sum);
        }
 
        for (int i = 0; i < outputSize; i++) {
            double sum = outputBias[i];
            for (int j = 0; j < hiddenSize; j++) {
                sum += outputWeights[i][j] * hiddenLayer[j];
            }
            outputLayer[i] = sigmoid(sum);
        }
 
        return outputLayer[0];
    }
};
 
int main() {
    int inputSize = 8;
    int outputSize = 1;
    int hiddenSize = 10;
    double learningRate = 0.1;
    int maxIterations = 10000;
 
    std::vector<std::vector<double>> inputs = {
        {1, 0, 1, 0, 1, 0, 1, 0},
        {0, 1, 0, 1, 0, 1, 0, 1},
        {0, 1, 1, 1, 0, 1, 0, 1},
        {1, 1, 1, 1, 0, 0, 0, 0},
        {0, 0, 0, 0, 1, 1, 1, 1}
    };
 
    std::vector<double> outputs = {1, 1, 0.7, 0, 0};
 
    NeuralNetwork network(inputSize, outputSize, hiddenSize, learningRate, maxIterations);
 
    network.train(inputs, outputs);
 
    // Beispiel für die Vorhersage mit neuen Daten
    std::vector<double> newInputs = {1, 1, 1, 0, 1, 0, 1, 0};
    double prediction = network.predict(newInputs);
 
    std::cout << "Prediction: " << prediction << std::endl;
 
    return 0;
}

Beispiel mit 3 Hidden Layer. Die Trainingsdaten sind die ASCII Werte der Klein und Großbuchstaben. Kleinbuchstaben werden schlecht und Großbuchstaben gut bewertet.

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
 
#define INPUT_SIZE 8
#define OUTPUT_SIZE 1
#define HIDDEN_SIZE_1 10
#define HIDDEN_SIZE_2 8
#define HIDDEN_SIZE_3 6
#define LEARNING_RATE 0.1
#define MAX_ITERATIONS 30000
 
double sigmoid(double x) {
    return 1.0 / (1.0 + exp(-x));
}
 
void train(double inputs[][INPUT_SIZE], double outputs[], int num_samples, double hidden_weights_1[][INPUT_SIZE], double hidden_weights_2[][HIDDEN_SIZE_1], double hidden_weights_3[][HIDDEN_SIZE_2], double output_weights[][HIDDEN_SIZE_3], double hidden_bias_1[], double hidden_bias_2[], double hidden_bias_3[], double output_bias[]) {
    double hidden_layer_1[HIDDEN_SIZE_1];
    double hidden_layer_2[HIDDEN_SIZE_2];
    double hidden_layer_3[HIDDEN_SIZE_3];
    double output_layer[OUTPUT_SIZE];
 
    // Zufällige Initialisierung der Gewichte und Biases
    for (int i = 0; i < HIDDEN_SIZE_1; i++) {
        hidden_bias_1[i] = ((double)rand() / RAND_MAX) * 2 - 1;
        for (int j = 0; j < INPUT_SIZE; j++) {
            hidden_weights_1[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
        }
    }
 
    for (int i = 0; i < HIDDEN_SIZE_2; i++) {
        hidden_bias_2[i] = ((double)rand() / RAND_MAX) * 2 - 1;
        for (int j = 0; j < HIDDEN_SIZE_1; j++) {
            hidden_weights_2[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
        }
    }
 
    for (int i = 0; i < HIDDEN_SIZE_3; i++) {
        hidden_bias_3[i] = ((double)rand() / RAND_MAX) * 2 - 1;
        for (int j = 0; j < HIDDEN_SIZE_2; j++) {
            hidden_weights_3[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
        }
    }
 
    for (int i = 0; i < OUTPUT_SIZE; i++) {
        output_bias[i] = ((double)rand() / RAND_MAX) * 2 - 1;
        for (int j = 0; j < HIDDEN_SIZE_3; j++) {
            output_weights[i][j] = ((double)rand() / RAND_MAX) * 2 - 1;
        }
    }
 
    // Trainingsschleife
    for (int iteration = 0; iteration < MAX_ITERATIONS; iteration++) {
        double total_error = 0.0;
 
        // Durchlaufen der Trainingsdaten
        for (int sample = 0; sample < num_samples; sample++) {
            // Vorwärtsdurchgang
            for (int i = 0; i < HIDDEN_SIZE_1; i++) {
                double sum = hidden_bias_1[i];
                for (int j = 0; j < INPUT_SIZE; j++) {
                    sum += hidden_weights_1[i][j] * inputs[sample][j];
                }
                hidden_layer_1[i] = sigmoid(sum);
            }
 
            for (int i = 0; i < HIDDEN_SIZE_2; i++) {
                double sum = hidden_bias_2[i];
                for (int j = 0; j < HIDDEN_SIZE_1; j++) {
                    sum += hidden_weights_2[i][j] * hidden_layer_1[j];
                }
                hidden_layer_2[i] = sigmoid(sum);
            }
 
            for (int i = 0; i < HIDDEN_SIZE_3; i++) {
                double sum = hidden_bias_3[i];
                for (int j = 0; j < HIDDEN_SIZE_2; j++) {
                    sum += hidden_weights_3[i][j] * hidden_layer_2[j];
                }
                hidden_layer_3[i] = sigmoid(sum);
            }
 
            for (int i = 0; i < OUTPUT_SIZE; i++) {
                double sum = output_bias[i];
                for (int j = 0; j < HIDDEN_SIZE_3; j++) {
                    sum += output_weights[i][j] * hidden_layer_3[j];
                }
                output_layer[i] = sigmoid(sum);
            }
 
            // Berechnung des Fehlers
            double error = outputs[sample] - output_layer[0];
            total_error += fabs(error);
 
            // Rückwärtsdurchgang
            double output_delta = error * output_layer[0] * (1.0 - output_layer[0]);
 
            for (int i = 0; i < HIDDEN_SIZE_3; i++) {
                double hidden_delta_3 = hidden_layer_3[i] * (1.0 - hidden_layer_3[i]) * output_delta * output_weights[0][i];
                int j;
                for (j = 0; j < HIDDEN_SIZE_2; j++) {
                    double hidden_delta_2 = hidden_layer_2[j] * (1.0 - hidden_layer_2[j]) * hidden_delta_3 * hidden_weights_3[i][j];
                    int k;
                    for (k = 0; k < HIDDEN_SIZE_1; k++) {
                        double hidden_delta_1 = hidden_layer_1[k] * (1.0 - hidden_layer_1[k]) * hidden_delta_2 * hidden_weights_2[j][k];
 
                        for (int l = 0; l < INPUT_SIZE; l++) {
                            hidden_weights_1[k][l] += LEARNING_RATE * hidden_delta_1 * inputs[sample][l];
                        }
                        hidden_bias_1[k] += LEARNING_RATE * hidden_delta_1;
                    }
 
                    hidden_weights_2[j][k] += LEARNING_RATE * hidden_delta_2 * hidden_layer_1[k];
                }
 
                hidden_weights_3[i][j] += LEARNING_RATE * hidden_delta_3 * hidden_layer_2[j];
            }
 
            for (int i = 0; i < OUTPUT_SIZE; i++) {
                for (int j = 0; j < HIDDEN_SIZE_3; j++) {
                    output_weights[i][j] += LEARNING_RATE * output_delta * hidden_layer_3[j];
                }
                output_bias[i] += LEARNING_RATE * output_delta;
            }
        }
 
        // Ausgabe des aktuellen Fehlers
        printf("Iteration: %d, Error: %f\n", iteration, total_error);
 
        // Abbruch, wenn der Fehler klein genug ist
        if (total_error < 0.01) {
            break;
        }
    }
}
 
double predict(double inputs[], double hidden_weights_1[][INPUT_SIZE], double hidden_weights_2[][HIDDEN_SIZE_1], double hidden_weights_3[][HIDDEN_SIZE_2], double output_weights[][HIDDEN_SIZE_3], double hidden_bias_1[], double hidden_bias_2[], double hidden_bias_3[], double output_bias[]) {
    double hidden_layer_1[HIDDEN_SIZE_1];
    double hidden_layer_2[HIDDEN_SIZE_2];
    double hidden_layer_3[HIDDEN_SIZE_3];
    double output_layer[OUTPUT_SIZE];
 
    // Vorwärtsdurchgang
    for (int i = 0; i < HIDDEN_SIZE_1; i++) {
        double sum = hidden_bias_1[i];
        for (int j = 0; j < INPUT_SIZE; j++) {
            sum += hidden_weights_1[i][j] * inputs[j];
        }
        hidden_layer_1[i] = sigmoid(sum);
    }
 
    for (int i = 0; i < HIDDEN_SIZE_2; i++) {
        double sum = hidden_bias_2[i];
        for (int j = 0; j < HIDDEN_SIZE_1; j++) {
            sum += hidden_weights_2[i][j] * hidden_layer_1[j];
        }
        hidden_layer_2[i] = sigmoid(sum);
    }
 
    for (int i = 0; i < HIDDEN_SIZE_3; i++) {
        double sum = hidden_bias_3[i];
        for (int j = 0; j < HIDDEN_SIZE_2; j++) {
            sum += hidden_weights_3[i][j] * hidden_layer_2[j];
        }
        hidden_layer_3[i] = sigmoid(sum);
    }
 
    for (int i = 0; i < OUTPUT_SIZE; i++) {
        double sum = output_bias[i];
        for (int j = 0; j < HIDDEN_SIZE_3; j++) {
            sum += output_weights[i][j] * hidden_layer_3[j];
        }
        output_layer[i] = sigmoid(sum);
    }
 
    return output_layer[0];
}
 
int byteToAscii(double byte[]) {
    int ascii = 0;
 
    for (int i = 0; i < 8; i++) {
        ascii += byte[i] * pow(2, 7 - i);
    }
 
    return ascii;
}
 
int main() {
    double inputs[][INPUT_SIZE] = {
// Kleinbuchstaben
        {0, 1, 1, 0, 0, 0, 0, 1},  // 'a' - 97
        {0, 1, 1, 0, 0, 0, 1, 0},  // 'b' - 98
        {0, 1, 1, 0, 0, 0, 1, 1},  // 'c' - 99
        {0, 1, 1, 0, 0, 1, 0, 0},  // 'd' - 100
        {0, 1, 1, 0, 0, 1, 0, 1},  // 'e' - 101
        {0, 1, 1, 0, 0, 1, 1, 0},  // 'f' - 102
        {0, 1, 1, 0, 0, 1, 1, 1},  // 'g' - 103
        {0, 1, 1, 0, 1, 0, 0, 0},  // 'h' - 104
        {0, 1, 1, 0, 1, 0, 0, 1},  // 'i' - 105
        {0, 1, 1, 0, 1, 0, 1, 0},  // 'j' - 106
        {0, 1, 1, 0, 1, 0, 1, 1},  // 'k' - 107
        {0, 1, 1, 0, 1, 1, 0, 0},  // 'l' - 108
        {0, 1, 1, 0, 1, 1, 0, 1},  // 'm' - 109
        {0, 1, 1, 0, 1, 1, 1, 0},  // 'n' - 110
        {0, 1, 1, 0, 1, 1, 1, 1},  // 'o' - 111
        {0, 1, 1, 1, 0, 0, 0, 0},  // 'p' - 112
        {0, 1, 1, 1, 0, 0, 0, 1},  // 'q' - 113
        {0, 1, 1, 1, 0, 0, 1, 0},  // 'r' - 114
        {0, 1, 1, 1, 0, 0, 1, 1},  // 's' - 115
        {0, 1, 1, 1, 0, 1, 0, 0},  // 't' - 116
        {0, 1, 1, 1, 0, 1, 0, 1},  // 'u' - 117
        {0, 1, 1, 1, 0, 1, 1, 0},  // 'v' - 118
        {0, 1, 1, 1, 0, 1, 1, 1},  // 'w' - 119
        {0, 1, 1, 1, 1, 0, 0, 0},  // 'x' - 120
        {0, 1, 1, 1, 1, 0, 0, 1},  // 'y' - 121
        {0, 1, 1, 1, 1, 0, 1, 0},  // 'z' - 122
 
        // Großbuchstaben
        {0, 1, 0, 0, 0, 0, 0, 1},  // 'A' - 65
        {0, 1, 0, 0, 0, 0, 1, 0},  // 'B' - 66
        {0, 1, 0, 0, 0, 0, 1, 1},  // 'C' - 67
        {0, 1, 0, 0, 0, 1, 0, 0},  // 'D' - 68
        {0, 1, 0, 0, 0, 1, 0, 1},  // 'E' - 69
        {0, 1, 0, 0, 0, 1, 1, 0},  // 'F' - 70
        {0, 1, 0, 0, 0, 1, 1, 1},  // 'G' - 71
        {0, 1, 0, 0, 1, 0, 0, 0},  // 'H' - 72
        {0, 1, 0, 0, 1, 0, 0, 1},  // 'I' - 73
        {0, 1, 0, 0, 1, 0, 1, 0},  // 'J' - 74
        {0, 1, 0, 0, 1, 0, 1, 1},  // 'K' - 75
        {0, 1, 0, 0, 1, 1, 0, 0},  // 'L' - 76
        {0, 1, 0, 0, 1, 1, 0, 1},  // 'M' - 77
        {0, 1, 0, 0, 1, 1, 1, 0},  // 'N' - 78
        {0, 1, 0, 0, 1, 1, 1, 1},  // 'O' - 79
 
 
        {0, 1, 0, 1, 0, 0, 0, 0},  // 'P' - 80
        {0, 1, 0, 1, 0, 0, 0, 1},  // 'Q' - 81
        {0, 1, 0, 1, 0, 0, 1, 0},  // 'R' - 82
        {0, 1, 0, 1, 0, 0, 1, 1},  // 'S' - 83
        {0, 1, 0, 1, 0, 1, 0, 0},  // 'T' - 84
        {0, 1, 0, 1, 0, 1, 0, 1},  // 'U' - 85
        {0, 1, 0, 1, 0, 1, 1, 0},  // 'V' - 86
        {0, 1, 0, 1, 0, 1, 1, 1},  // 'W' - 87
        {0, 1, 0, 1, 1, 0, 0, 0},  // 'X' - 88
        {0, 1, 0, 1, 1, 0, 0, 1},  // 'Y' - 89
        {0, 1, 0, 1, 1, 0, 1, 0}  // 'Z' - 90
    };
    double outputs[] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1};
    size_t totalSize = sizeof(inputs) / sizeof(inputs[0]);
    int num_samples = totalSize;
 
    double hidden_weights_1[HIDDEN_SIZE_1][INPUT_SIZE];
    double hidden_weights_2[HIDDEN_SIZE_2][HIDDEN_SIZE_1];
    double hidden_weights_3[HIDDEN_SIZE_3][HIDDEN_SIZE_2];
    double output_weights[OUTPUT_SIZE][HIDDEN_SIZE_3];
    double hidden_bias_1[HIDDEN_SIZE_1];
    double hidden_bias_2[HIDDEN_SIZE_2];
    double hidden_bias_3[HIDDEN_SIZE_3];
    double output_bias[OUTPUT_SIZE];
 
    train(inputs, outputs, num_samples, hidden_weights_1, hidden_weights_2, hidden_weights_3, output_weights, hidden_bias_1, hidden_bias_2, hidden_bias_3, output_bias);
 
    // Testen des trainierten Modells
    double test_input[] = {0, 1, 1, 1, 0, 1, 1, 0};
    double prediction = predict(test_input, hidden_weights_1, hidden_weights_2, hidden_weights_3, output_weights, hidden_bias_1, hidden_bias_2, hidden_bias_3, output_bias);
 
    int ascii_value = byteToAscii(test_input);
 
 
    printf("Input: %c - Prediction: %f\n", (char)ascii_value, prediction);
 
    return 0;
}

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <string.h>
 
#define INPUT_COUNT 5
#define HIDDEN_COUNT 5
#define OUTPUT_COUNT 1
 
#define LEARNING_RATE 0.15
 
typedef struct
{
  float in_Weights[INPUT_COUNT];
  float inBias;
  float value;
  float out_Weights[OUTPUT_COUNT];
}Neuron;
 
typedef struct
{
  float value;
}IO_Neuron;
 
typedef struct
{
  int sucess;
  IO_Neuron** training_in;
  IO_Neuron** training_out;
  int examples;
}TData;
//loads training data from a file like format below
/*
  #inputs,outputs,count
  input1,input2,input3 output1,output2
*/
TData tData(const char* filename)
{
  FILE* fp = fopen(filename,"r");
  int ins,outs,count;
  fscanf(fp,"#%i,%i,%i",&ins,&outs,&count);
  TData ret;
  ret.sucess = 1;
  if (ins != INPUT_COUNT || outs != OUTPUT_COUNT)
  {
    printf("%s\n","File will not fit into network!" );
    ret.sucess = 0;
    return ret;
  }
 
 
  int i,j;
  ret.training_in = malloc(sizeof(IO_Neuron*)*count);
  ret.training_out = malloc(sizeof(IO_Neuron*)*count);
  ret.examples = count;
  for (i =0; i< count;i++)
  {
    ret.training_in[i] = malloc(sizeof(IO_Neuron)*INPUT_COUNT);
  }
 
  for (i =0; i< count;i++)
  {
    ret.training_out[i] = malloc(sizeof(IO_Neuron)*OUTPUT_COUNT);
  }
 
  for (i =0 ; i < count;i++)
  {
    int inIndex = 0;
    int outIndex = 0;
    for (j =0; j < (INPUT_COUNT*2 - 1);j++)
    {
      if (j % 2 == 1)
      {
        fscanf(fp,",");
      }
      else
      {
        fscanf(fp,"%f",&ret.training_in[i][inIndex]);
        inIndex += 1;
      }
    }
    fscanf(fp," ");
    for (j =0; j < (OUTPUT_COUNT*2 - 1);j++)
    {
      if (j % 2 == 1)
      {
        fscanf(fp,",");
      }
      else
      {
        fscanf(fp,"%f",&ret.training_out[i][outIndex]);
        outIndex += 1;
      }
    }
  }
  printf("%s\n","File Read Sucessfully!" );
  return ret;
 
}
 
float genRandRange(float min,float max)
{
  if (min == max)
  return min;
  float scale = rand() / (float) RAND_MAX; /* [0, 1.0] */
  return min + scale * ( max - min );      /* [min, max] */
}
 
//activation function
float sigmoid(float x)
{
  return 1 / (1 + exp(-x));
}
 
float sigmoid_derivative(float x)
{
  return sigmoid(x) * (1 - sigmoid(x));
}
 
//computes weighted sum
float dot_summation(float* in,float* weights,int count)
{
  int i;
  float result = 0;
  for (i =0;i < count;i++)
  {
    result += in[i]*weights[i];
  }
  return result;
}
 
//these functions extract data into an easier to handle format
float* ioValues(IO_Neuron* hidden_layer)
{
  float* ret = malloc(sizeof(float)*INPUT_COUNT);
  int i;
  for (i =0; i < INPUT_COUNT;i++)
  {
    ret[i] = hidden_layer[i].value;
  }
  return ret;
}
 
float* values(Neuron* hidden_layer)
{
  float* ret = malloc(sizeof(float)*HIDDEN_COUNT);
  int i;
  for (i =0; i < HIDDEN_COUNT;i++)
  {
    ret[i] = hidden_layer[i].value;
  }
  return ret;
}
 
float* outWeights(Neuron* hidden_layer,int index)
{
  float* ret = malloc(sizeof(float)*HIDDEN_COUNT);
  int i;
  for (i =0; i < HIDDEN_COUNT;i++)
  {
    ret[i] = hidden_layer[i].out_Weights[index];
  }
  return ret;
}
 
//pass values through the neural network
void think(IO_Neuron* input_layer,Neuron* hidden_layer,IO_Neuron* output_layer)
{
  int i;
  float* io_values = ioValues(input_layer);
  for (i =0; i < HIDDEN_COUNT;i++)
  {
    hidden_layer[i].value = sigmoid(dot_summation(io_values,hidden_layer[i].in_Weights,INPUT_COUNT) + hidden_layer[i].inBias);
  }
  free(io_values);
 
  float* hidden_values = values(hidden_layer);
  for (i =0; i < OUTPUT_COUNT;i++)
  {
    float* out_weights = outWeights(hidden_layer,i);
    output_layer[i].value = sigmoid(dot_summation(hidden_values,out_weights,HIDDEN_COUNT));
    free(out_weights);
  }
  free(hidden_values);
 
}
 
//adjust the neural network's connection weights and biases based upon training data
void train(IO_Neuron* input_layer,Neuron* hidden_layer,IO_Neuron* output_layer,IO_Neuron** input_training,IO_Neuron** output_training,int training_samples,int iterations)
{
  int i,j,k,l;
  IO_Neuron recorded_outputs[training_samples][OUTPUT_COUNT];
  Neuron recorded_hidden[training_samples][HIDDEN_COUNT];
  float error_output[training_samples][OUTPUT_COUNT];//contains output node's delta
  float error_hidden[training_samples][HIDDEN_COUNT];
  for (i =0; i < iterations;i++)
  {
    for (j =0; j < training_samples;j++)
    {
      think(input_training[j],hidden_layer,output_layer);
      memcpy(recorded_outputs[j],output_layer,sizeof(IO_Neuron)*OUTPUT_COUNT);
      memcpy(recorded_hidden[j],hidden_layer,sizeof(Neuron)*HIDDEN_COUNT);
    }
 
    for (j =0; j < training_samples;j++)
    {
      for (k =0; k < OUTPUT_COUNT;k++)
      {
        error_output[j][k] = recorded_outputs[j][k].value*(1 - recorded_outputs[j][k].value) * (output_training[j][k].value - recorded_outputs[j][k].value);
      }
    }
    for (j =0; j < training_samples;j++)
    {
      for (k =0; k < HIDDEN_COUNT;k++)
      {
        float errorFactor = 0;
        for (l =0;l < OUTPUT_COUNT;l++)
        {
          errorFactor += (error_output[j][l]*hidden_layer[k].out_Weights[l]);
        }
        error_hidden[j][k] = recorded_hidden[j][k].value*(1 - recorded_hidden[j][k].value) * errorFactor;
      }
    }
 
    for (j =0; j < training_samples;j++)
    {
      for (k =0; k < HIDDEN_COUNT;k++)
      {//TODO update biases
        hidden_layer[k].inBias = hidden_layer[k].inBias + LEARNING_RATE *error_hidden[j][k];
        for (l = 0;l < INPUT_COUNT;l++)
        {
          hidden_layer[k].in_Weights[l] = hidden_layer[k].in_Weights[l] + (LEARNING_RATE*error_hidden[j][k]*input_training[j][l].value)/training_samples;
        }
      }
    }
 
    for (j =0; j < training_samples;j++)
    {
      for (k =0; k < HIDDEN_COUNT;k++)
      {
        for (l = 0;l < OUTPUT_COUNT;l++)
        {
          hidden_layer[k].out_Weights[l] = hidden_layer[k].out_Weights[l] + (LEARNING_RATE*error_output[j][k]*recorded_hidden[j][k].value)/training_samples;
        }
      }
    }
 
 
 
  }
}
 
//assign random weights to the neural network's connections
void randweights(Neuron* neurons)
{
  int i;
  for (i =0;i< HIDDEN_COUNT;i++)
  {
    neurons[i].in_Weights[0] = 2*genRandRange(0,1) - 1;
    neurons[i].in_Weights[1] = 2*genRandRange(0,1) - 1;
    neurons[i].in_Weights[2] = 2*genRandRange(0,1) - 1;
 
    neurons[i].out_Weights[2] = 2*genRandRange(0,1) - 1;
 
    neurons[i].inBias = 2*genRandRange(0,1) - 1;
  }
}
 
int main()
{
 
  srand(1);
  int i,j;
  //aquire training data
  TData t_data = tData("training.txt");
  if (!t_data.sucess)
  {
    return 0;
  }
  IO_Neuron** training_in = t_data.training_in;
  IO_Neuron** training_out = t_data.training_out;
 
  //allocate neural network
  IO_Neuron* input_layer = malloc(sizeof(IO_Neuron)*INPUT_COUNT);
  Neuron* hidden_layer = malloc(sizeof(Neuron)*HIDDEN_COUNT);
  IO_Neuron* output_layer = malloc(sizeof(IO_Neuron)*OUTPUT_COUNT);
 
  randweights(hidden_layer);
 
  //train with training data
  train(input_layer,hidden_layer,output_layer,training_in,training_out,t_data.examples,100000);
 
  //test out the learned pattern
  input_layer[0].value = 0;
  input_layer[1].value = 0;
  input_layer[2].value = 0;
  input_layer[3].value = 0;
  input_layer[4].value = 1;
 
  //generates the output
  think(input_layer,hidden_layer,output_layer);
 
  for (i =0; i < OUTPUT_COUNT;i++)
  {
    printf("%f\n",output_layer[i].value );
  }
  return 0;
}

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <string.h>
 
#define INPUT_COUNT 5
#define HIDDEN_LAYER_COUNT 5  // Anzahl der Hidden Layer
#define HIDDEN_COUNT 5
#define OUTPUT_COUNT 1
 
#define LEARNING_RATE 0.15
 
typedef struct
{
  float in_Weights[INPUT_COUNT];
  float inBias;
  float value;
  float out_Weights[OUTPUT_COUNT];
} Neuron;
 
typedef struct
{
  float value;
} IO_Neuron;
 
typedef struct
{
  int success;
  IO_Neuron** training_in;
  IO_Neuron** training_out;
  int examples;
} TData;
 
//loads training data from a file like format below
/*
  #inputs,outputs,count
  input1,input2,input3 output1,output2
*/
TData tData(const char* filename)
{
  FILE* fp = fopen(filename,"r");
  int ins,outs,count;
  fscanf(fp,"#%i,%i,%i",&ins,&outs,&count);
  TData ret;
  ret.success = 1;
  if (ins != INPUT_COUNT || outs != OUTPUT_COUNT)
  {
    printf("%s\n","File will not fit into network!" );
    ret.success = 0;
    return ret;
  }
 
 
  int i,j;
  ret.training_in = malloc(sizeof(IO_Neuron*)*count);
  ret.training_out = malloc(sizeof(IO_Neuron*)*count);
  ret.examples = count;
  for (i =0; i< count;i++)
  {
    ret.training_in[i] = malloc(sizeof(IO_Neuron)*INPUT_COUNT);
  }
 
  for (i =0; i< count;i++)
  {
    ret.training_out[i] = malloc(sizeof(IO_Neuron)*OUTPUT_COUNT);
  }
 
  for (i =0 ; i < count;i++)
  {
    int inIndex = 0;
    int outIndex = 0;
    for (j =0; j < (INPUT_COUNT*2 - 1);j++)
    {
      if (j % 2 == 1)
      {
        fscanf(fp,",");
      }
      else
      {
        fscanf(fp,"%f",&ret.training_in[i][inIndex].value);
        inIndex += 1;
      }
    }
    fscanf(fp," ");
    for (j =0; j < (OUTPUT_COUNT*2 - 1);j++)
    {
      if (j % 2 == 1)
      {
        fscanf(fp,",");
      }
      else
      {
        fscanf(fp,"%f",&ret.training_out[i][outIndex].value);
        outIndex += 1;
      }
    }
  }
  printf("%s\n","File Read Successfully!" );
  return ret;
 
}
 
float genRandRange(float min,float max)
{
  if (min == max)
    return min;
  float scale = rand() / (float) RAND_MAX; /* [0, 1.0] */
  return min + scale * ( max - min );      /* [min, max] */
}
 
float sigmoid(float x)
{
  return 1 / (1 + exp(-x));
}
 
float sigmoid_derivative(float x)
{
  return sigmoid(x) * (1 - sigmoid(x));
}
 
float dot_summation(float* in,float* weights,int count)
{
  int i;
  float result = 0;
  for (i =0;i < count;i++)
  {
    result += in[i]*weights[i];
  }
  return result;
}
 
float* ioValues(IO_Neuron* hidden_layer)
{
  float* ret = malloc(sizeof(float)*INPUT_COUNT);
  int i;
  for (i =0; i < INPUT_COUNT;i++)
  {
    ret[i] = hidden_layer[i].value;
  }
  return ret;
}
 
float* values(Neuron* hidden_layer)
{
  float* ret = malloc(sizeof(float)*HIDDEN_COUNT);
  int i;
  for (i =0; i < HIDDEN_COUNT;i++)
  {
    ret[i] = hidden_layer[i].value;
  }
  return ret;
}
 
float* outWeights(Neuron* hidden_layer,int index)
{
  float* ret = malloc(sizeof(float)*HIDDEN_COUNT);
  int i;
  for (i =0; i < HIDDEN_COUNT;i++)
  {
    ret[i] = hidden_layer[i].out_Weights[index];
  }
  return ret;
}
 
void think(IO_Neuron* input_layer, Neuron** hidden_layers, IO_Neuron* output_layer)
{
  float* io_values = ioValues(input_layer);
 
  for (int i = 0; i < HIDDEN_LAYER_COUNT; i++) {
    float* hidden_values = values(hidden_layers[i]);
 
    for (int j = 0; j < HIDDEN_COUNT; j++) {
      hidden_layers[i][j].value = sigmoid(dot_summation(io_values, hidden_layers[i][j].in_Weights, INPUT_COUNT) + hidden_layers[i][j].inBias);
    }
 
    if (i < HIDDEN_LAYER_COUNT - 1) {
      float* next_hidden_values = values(hidden_layers[i + 1]);
 
      for (int j = 0; j < HIDDEN_COUNT; j++) {
        float* out_weights = outWeights(hidden_layers[i], j);
 
        for (int k = 0; k < HIDDEN_COUNT; k++) {
          hidden_layers[i + 1][k].value = sigmoid(dot_summation(hidden_values, out_weights, HIDDEN_COUNT));
        }
 
        free(out_weights);
      }
 
      free(next_hidden_values);
    }
 
    free(hidden_values);
  }
 
  float* hidden_values = values(hidden_layers[HIDDEN_LAYER_COUNT - 1]);
 
  for (int i = 0; i < OUTPUT_COUNT; i++) {
    float* out_weights = outWeights(hidden_layers[HIDDEN_LAYER_COUNT - 1], i);
 
    output_layer[i].value = sigmoid(dot_summation(hidden_values, out_weights, HIDDEN_COUNT));
 
    free(out_weights);
  }
 
  free(io_values);
  free(hidden_values);
}
 
void train(IO_Neuron* input_layer, Neuron** hidden_layers, IO_Neuron* output_layer, IO_Neuron** input_training, IO_Neuron** output_training, int training_samples, int iterations)
{
  IO_Neuron recorded_outputs[training_samples][OUTPUT_COUNT];
  Neuron recorded_hidden[HIDDEN_LAYER_COUNT][training_samples][HIDDEN_COUNT];
  float error_output[training_samples][OUTPUT_COUNT];
  float error_hidden[HIDDEN_LAYER_COUNT][training_samples][HIDDEN_COUNT];
 
  for (int i = 0; i < iterations; i++)
  {
    for (int j = 0; j < training_samples; j++)
    {
      think(input_training[j], hidden_layers, output_layer);
 
      for (int k = 0; k < OUTPUT_COUNT; k++) {
        recorded_outputs[j][k] = output_layer[k];
      }
 
      for (int l = 0; l < HIDDEN_LAYER_COUNT; l++) {
        for (int m = 0; m < HIDDEN_COUNT; m++) {
          recorded_hidden[l][j][m] = hidden_layers[l][m];
        }
      }
    }
 
    for (int j = 0; j < training_samples; j++)
    {
      for (int k = 0; k < OUTPUT_COUNT; k++)
      {
        error_output[j][k] = recorded_outputs[j][k].value * (1 - recorded_outputs[j][k].value) * (output_training[j][k].value - recorded_outputs[j][k].value);
      }
    }
 
    for (int j = 0; j < training_samples; j++)
    {
      for (int l = HIDDEN_LAYER_COUNT - 1; l >= 0; l--)
      {
        for (int m = 0; m < HIDDEN_COUNT; m++)
        {
          float errorFactor = 0;
 
          if (l < HIDDEN_LAYER_COUNT - 1)
          {
            for (int n = 0; n < HIDDEN_COUNT; n++)
            {
              errorFactor += (error_hidden[l + 1][j][n] * hidden_layers[l][m].out_Weights[n]);
            }
          }
          else
          {
            for (int n = 0; n < OUTPUT_COUNT; n++)
            {
              errorFactor += (error_output[j][n] * hidden_layers[l][m].out_Weights[n]);
            }
          }
 
          error_hidden[l][j][m] = recorded_hidden[l][j][m].value * (1 - recorded_hidden[l][j][m].value) * errorFactor;
        }
      }
    }
 
    for (int j = 0; j < training_samples; j++)
    {
      for (int l = HIDDEN_LAYER_COUNT - 1; l >= 0; l--)
      {
        for (int m = 0; m < HIDDEN_COUNT; m++)
        {
          hidden_layers[l][m].inBias += LEARNING_RATE * error_hidden[l][j][m];
 
          if (l > 0)
          {
            for (int n = 0; n < HIDDEN_COUNT; n++)
            {
              hidden_layers[l][m].in_Weights[n] += (LEARNING_RATE * error_hidden[l][j][m] * recorded_hidden[l - 1][j][n].value) / training_samples;
            }
          }
          else
          {
            for (int n = 0; n < INPUT_COUNT; n++)
            {
              hidden_layers[l][m].in_Weights[n] += (LEARNING_RATE * error_hidden[l][j][m] * input_training[j][n].value) / training_samples;
            }
          }
        }
      }
    }
 
    for (int j = 0; j < training_samples; j++)
    {
      for (int l = HIDDEN_LAYER_COUNT - 1; l >= 0; l--)
      {
        for (int m = 0; m < HIDDEN_COUNT; m++)
        {
          if (l < HIDDEN_LAYER_COUNT - 1)
          {
            for (int n = 0; n < HIDDEN_COUNT; n++)
            {
              hidden_layers[l][m].out_Weights[n] += (LEARNING_RATE * error_hidden[l + 1][j][m] * recorded_hidden[l][j][m].value) / training_samples;
            }
          }
          else
          {
            for (int n = 0; n < OUTPUT_COUNT; n++)
            {
              hidden_layers[l][m].out_Weights[n] += (LEARNING_RATE * error_output[j][n] * recorded_hidden[l][j][m].value) / training_samples;
            }
          }
        }
      }
    }
  }
}
 
void randweights(Neuron** hidden_layers)
{
  for (int i = 0; i < HIDDEN_LAYER_COUNT; i++)
  {
    for (int j = 0; j < HIDDEN_COUNT; j++)
    {
      hidden_layers[i][j].in_Weights[0] = 2 * genRandRange(0, 1) - 1;
      hidden_layers[i][j].in_Weights[1] = 2 * genRandRange(0, 1) - 1;
      hidden_layers[i][j].in_Weights[2] = 2 * genRandRange(0, 1) - 1;
 
      if (i < HIDDEN_LAYER_COUNT - 1)
      {
        hidden_layers[i][j].out_Weights[2] = 2 * genRandRange(0, 1) - 1;
      }
    }
    hidden_layers[i][0].inBias = 2 * genRandRange(0, 1) - 1;
  }
}
 
int main(int argc, char **argv)
{
  srand(1);
 
  TData t_data = tData("training.txt");
  if (!t_data.success)
  {
    return 0;
  }
  IO_Neuron** training_in = t_data.training_in;
  IO_Neuron** training_out = t_data.training_out;
 
  IO_Neuron* input_layer = malloc(sizeof(IO_Neuron) * INPUT_COUNT);
  Neuron** hidden_layers = malloc(sizeof(Neuron*) * HIDDEN_LAYER_COUNT);
  for (int i = 0; i < HIDDEN_LAYER_COUNT; i++)
  {
    hidden_layers[i] = malloc(sizeof(Neuron) * HIDDEN_COUNT);
  }
  IO_Neuron* output_layer = malloc(sizeof(IO_Neuron) * OUTPUT_COUNT);
 
  randweights(hidden_layers);
 
  train(input_layer, hidden_layers, output_layer, training_in, training_out, t_data.examples, 100000);
 
  input_layer[0].value = 0;
  input_layer[1].value = 0;
  input_layer[2].value = 1;
  input_layer[3].value = 0;
  input_layer[4].value = 0;
 
  think(input_layer, hidden_layers, output_layer);
 
  for (int i = 0; i < OUTPUT_COUNT; i++)
  {
    printf("%f\n", output_layer[i].value);
  }
 
  return 0;
}

• Neural network/Machine learning playlist
• Machine Learning for Everybody – Full Course