Inhaltsverzeichnis
Die Trigonometrie beschäftigt sich hauptsächlich mit den trigonometrischen Funktionen, die das Verhältnis der Seitenlängen eines rechtwinkligen Dreiecks zu den Winkeln in diesem Dreieck beschreiben. Trigonometrie ist ein wesentlicher Bestandteil von Game Engines. Die drei wichtigsten trigonometrischen Funktionen sind:
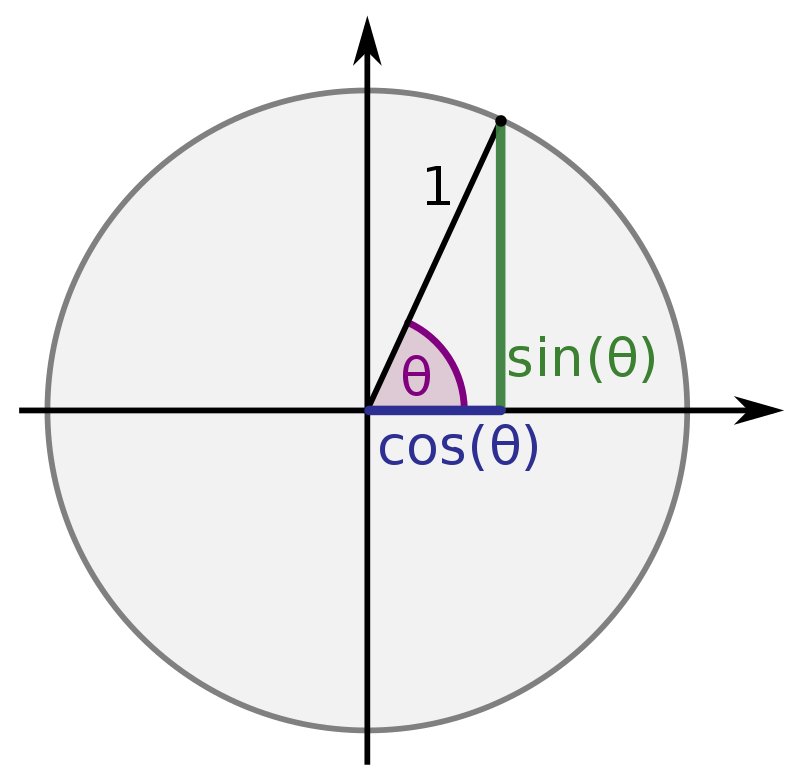
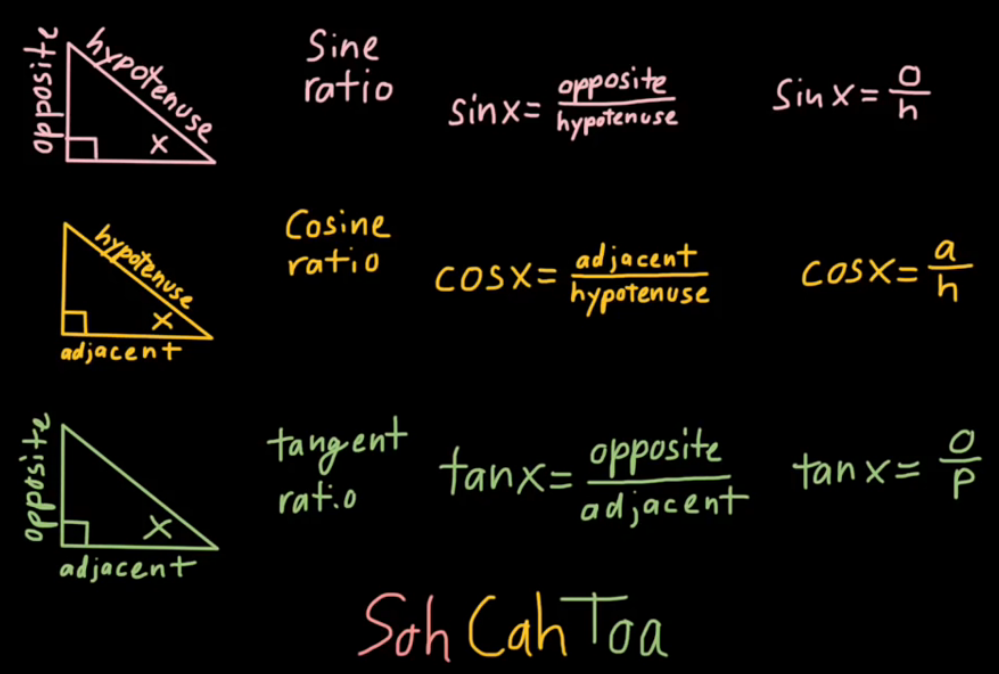
- Sinus (sin): Das Verhältnis der Länge der dem Winkel gegenüberliegenden Seite zur Hypotenuse des Dreiecks.
- Kosinus (cos): Das Verhältnis der Länge der anliegenden Seite zur Hypotenuse des Dreiecks.
- Tangens (tan): Das Verhältnis des Sinus zum Kosinus eines Winkels.
Zusätzlich zu diesen Funktionen gibt es auch ihre inversen Funktionen, den Arcussinus (asin), Arkuskosinus (acos) und Arkustangens (atan), die das Verhältnis von Seitenlängen zu Winkeln berechnen.
Es gibt die ebene und die sphärische Trigonometrie. Der Kosinussatz wird auch als trigonometrischer Pythagoras bezeichnet. Das rührt daher, daß mit ihm wie beim Satz des Pythagoras eine fehlende Dreieckseite berechnet werden kann, allerdings im Gegensatz zum Pythagoras, der ja nur für rechtwinklige Dreiecke gilt, in jedem beliebigen Dreieck. Siehe auch Vektor und Matrixmanipulation (Youtube).
- Innenwinkelsumme: 180°
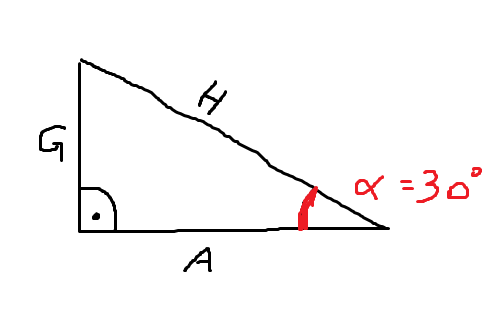
- Ankathete - am Winkel - Cosinus
- Gegenkathete - gegenüber vom Winkel - Sinus
- sin und cos müssen < 1.0 sein - tan nicht!
Merke Das Längenverhältnis aus Gegenkathete(alpha) und Hypotenuse ist sin(alpha)
sin(a) = Gegenkathete / Hypothenuse => G = H * sin(a) cos(a) = Ankathete / Hypothenuse => A = H * cos(a) tan(a) = Gegenkathete / Ankathete
Spieleentwicklung
Bewegungen
Die Berechnung von Bewegungen mit Vektoren ist in der Spieleentwicklung sehr gebräuchlich und ermöglicht eine präzise Steuerung von Objekten im Raum. Hier sind einige grundlegende Schritte zur Berechnung von Bewegungen mit Vektoren:
- Vektorrepräsentation: Ein Objekt wird in der Regel durch einen Positionsvektor repräsentiert, der seine aktuelle Position im Raum angibt. Dieser Vektor besteht aus den Koordinaten (x, y, z) des Objekts.
- Geschwindigkeitsvektor: Um die Bewegung des Objekts darzustellen, wird ein Geschwindigkeitsvektor definiert. Dieser Vektor gibt die Richtung und Geschwindigkeit an, in der sich das Objekt bewegt. Der Geschwindigkeitsvektor kann ebenfalls die Koordinaten (vx, vy, vz) haben.
- Aktualisierung der Position: Um die Position des Objekts zu aktualisieren, wird der Geschwindigkeitsvektor auf den Positionsvektor addiert. Dies wird normalerweise in kleinen Schritten über die Zeit durchgeführt. Die neue Position des Objekts wird dann berechnet als:
neue_Position = alte_Position + Geschwindigkeitsvektor * Zeit
- Beschleunigung: Um eine Beschleunigung zu berücksichtigen, kann ein weiterer Vektor, der Beschleunigungsvektor, verwendet werden. Der Beschleunigungsvektor gibt die Änderung der Geschwindigkeit pro Zeiteinheit an. Die Geschwindigkeit wird dann entsprechend der Beschleunigung angepasst:
neue_Geschwindigkeit = alte_Geschwindigkeit + Beschleunigungsvektor * Zeit
- Kollisionserkennung und -behandlung: Bei der Bewegung von Objekten müssen Kollisionen mit anderen Objekten oder Grenzen berücksichtigt werden. Trigonometrie wird verwendet, um Kollisionsbedingungen zu überprüfen und entsprechende Maßnahmen zu ergreifen, wie beispielsweise die Reflexion des Objekts an einer Oberfläche oder das Stoppen der Bewegung.
Bei der Berechnung von Bewegungen mit Vektoren können trigonometrische Funktionen verwendet werden, um die Richtung und Geschwindigkeit von Objekten zu steuern. Zusätzlich können Konzepte wie Skalare Multiplikation, Vektoraddition und Skalarprodukt in den Berechnungen angewendet werden.
Rotationen
Um Drehungen mit Vektoren zu berechnen, werden Matrizenoperationen verwendet. Die grundlegende Methode besteht darin, den Vektor mit einer Rotationsmatrix zu multiplizieren. Die Rotationsmatrix hängt von der Art der Drehung ab, z. B. einer Drehung um die x-, y- oder z-Achse.
Vektorrepräsentation: Der zu drehende Vektor wird als Spaltenvektor dargestellt.
[x] [y] [z]
Auswahl der Rotationsachse: Entscheiden Sie, um welche Achse Sie den Vektor drehen möchten. Mögliche Optionen sind x-, y- oder z-Achse.
Rotationsmatrix
Abhängig von der ausgewählten Achse wird eine entsprechende Rotationsmatrix erstellt. Hier sind die Rotationsmatrizen für die drei Hauptachsen:
Drehung um die x-Achse (Roll):
[ 1 0 0 ] [ 0 cosθ -sinθ ] [ 0 sinθ cosθ ]
Drehung um die y-Achse (Gier):
[ cosθ 0 sinθ ] [ 0 1 0 ] [-sinθ 0 cosθ ]
Drehung um die z-Achse (Nick):
[ cosθ -sinθ 0 ] [ sinθ cosθ 0 ] [ 0 0 1 ]
Hierbei ist θ (Theta) der Drehwinkel.
Multiplikation der Rotationsmatrix mit dem Vektor: Der ursprüngliche Vektor wird mit der entsprechenden Rotationsmatrix multipliziert, um den rotierten Vektor zu erhalten. Die Reihenfolge der Multiplikation kann je nach Anwendung variieren.
[x_rot] [y_rot] [z_rot] = Rotationsmatrix * [x] [y] [z]
Der resultierende Vektor [x_rot, y_rot, z_rot] ist der rotierte Vektor. Durch Anwendung verschiedener Drehwinkel und Kombinationen von Rotationsmatrizen können komplexe Drehungen und Transformationen von Vektoren erreicht werden.
Es ist zu beachten, dass diese Methode die Verwendung von homogenen Koordinaten und die Kombination von Rotations- und Translationsmatrizen für komplexere Transformationen nicht abdeckt. In solchen Fällen werden Matrizenoperationen wie Matrixmultiplikation und Transposition verwendet, um die gewünschten Transformationen zu berechnen.
Videos
- https://www.youtube.com/watch?v=xvvRdQtwFN4 (Lehrer Schmitd: Sinus)
- https://www.youtube.com/watch?v=iBBfU2zv0tw (Lehrer Schmitd: Kosinus)
- https://www.youtube.com/watch?v=yWDxBnc6XRU (Geschichte)
- https://www.youtube.com/watch?v=NQGywH7yrTw Large angles
allgemeines Dreieck
Kosinussatz
Links
- Rotation matrizes https://www.youtube.com/watch?v=OYuoPTRVzxY
- Trigonometry in Games https://www.youtube.com/watch?v=-dGi2Ffdiuk
- 2D 3D Trig https://www.youtube.com/watch?v=l2dn6ZygAkQ
- Math is fun https://www.mathsisfun.com