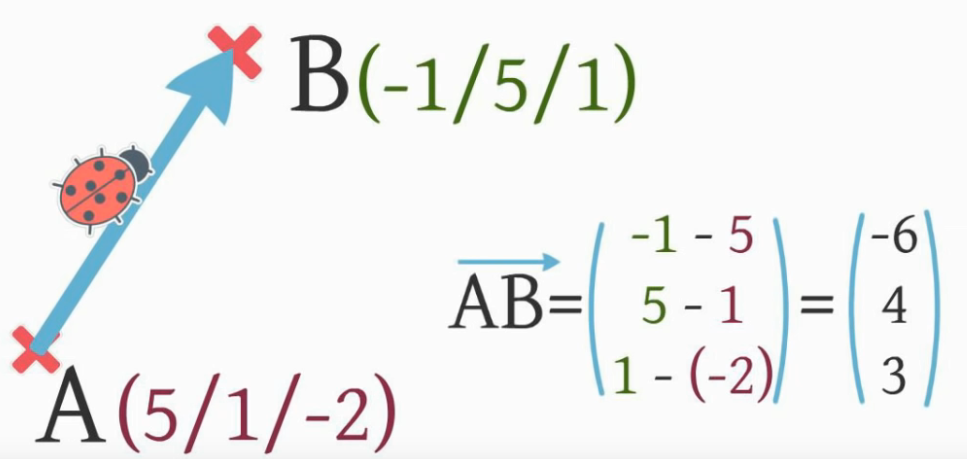Benutzer-Werkzeuge
Dies ist eine alte Version des Dokuments!
Inhaltsverzeichnis
Punkte in einem 3 dimensionalen Raum (Koordinaten) werden in einer Zeile dargestellt, die Wege zu den Punkten (Vektor) untereinander. (siehe Trigonometrie bzw Matrixmanipulation (Youtube))
https://www.youtube.com/watch?v=rowWM-MijXU
KoordinateA = (1,2,3)
1
VektorB = 2
3
Verschiedene Arten und was man dadurch erhält.
Vektoren addieren
Vektoraddition und -subtraktion sind grundlegende Operationen, um die Bewegung von Objekten im Raum zu berechnen. Durch die Addition eines Vektors zu einem anderen Vektor kann die Position eines Objekts aktualisiert werden. Die Subtraktion zweier Vektoren ermöglicht die Berechnung der Verschiebung zwischen zwei Positionen.
- Jede Zeile miteinander addieren, das Ergebnis ist ein neuer Vektor.
- Man kann einen Vektor NICHT mit einem Skalar addieren (undefined).
2
VectorA = 3
4
3
VectorB = 4
5
2 3 5
VectorC = 3 + 4 = 7
4 5 9
Vektoren multiplizieren
Skalarprodukt
Das Skalarprodukt (auch bekannt als Punktprodukt) wird verwendet, um den Winkel zwischen zwei Vektoren zu berechnen. Es ist auch nützlich, um die Geschwindigkeit eines Objekts in eine bestimmte Richtung zu bestimmen oder um zu überprüfen, ob zwei Objekte aufeinander zubewegt werden.
Kreuzprodukt
Das Kreuzprodukt (auch bekannt als Vektorprodukt) wird in der dreidimensionalen Geometrie verwendet, um einen neuen Vektor zu erzeugen, der senkrecht auf den beiden Ausgangsvektoren steht. Es ist nützlich für die Berechnung von Oberflächennormalen, Reflexionen und Rotationen in dreidimensionalen Spielen.
Vektorlänge und Normalisierung
Die Länge eines Vektors kann berechnet werden, indem die Wurzel der Summe der Quadrate seiner Komponenten genommen wird. Dies ist nützlich, um die Geschwindigkeit eines Objekts zu bestimmen oder um zu überprüfen, ob ein Objekt eine bestimmte Reichweite erreicht hat. Die Normalisierung eines Vektors bedeutet, ihn auf eine Länge von 1 zu skalieren, während seine Richtung beibehalten wird. Dies ist hilfreich, um Kollisionsprüfungen durchzuführen oder um Richtungen und Kräfte zu normalisieren.
Vektoren multiplizieren
- Multipliziert man einen Vektor und ein Skalar erhält man einen neuen Vektor - multipliziert man 2 Vektoren erhält man ein Skalarprodukt (normale Zahl).
- Multiplikation ändert nur die Länge, NICHT die Richtung!
2
VectorA = 3
4
2 6
VectorB = 3 * 3 = 9
4 12
2 3
VectorC = 3 * 4 = 2 * 3 + 3 * 4 + 4 * 5 = 38
4 5
- Multipliziert man 2 Vektoren und erhält 0 als Ergebnis, sind diese orthogonal (stehen im rechten Winkel aufeinander).
- Besonders wichtig in der 3D Programmierung ist das Kreuzprodukt, damit kann man nämlich ermitteln ob die 3. Achse im rechten Winkel zu den 2 ersten Achsen steht!
Dot product
siehe auch Lighthouse3D Dot product
Das Skalarprodukt berechnet eine Normale auf eine Gerade. Sozusagen die 2. Dimension.
Hat man 2 Koordinaten gegeben und möchste den Weg dahin definieren stellt man einen Vektor auf. Man subtrahiert ZIEL - START - nicht umgekehrt!!!
Das bedeutet umgekehrt - möchte man von A(5, 1, -2) nach B(-1, 5, 1)
Von 5 nach -1 => -6 Von 1 nach 5 => 4 Von -2 nach 1 => 3
Merke:
- if dot > 0 ⇒ deg < 90
- if dot == 0 ⇒ deg == 90
- if dot < 0 ⇒ deg > 90
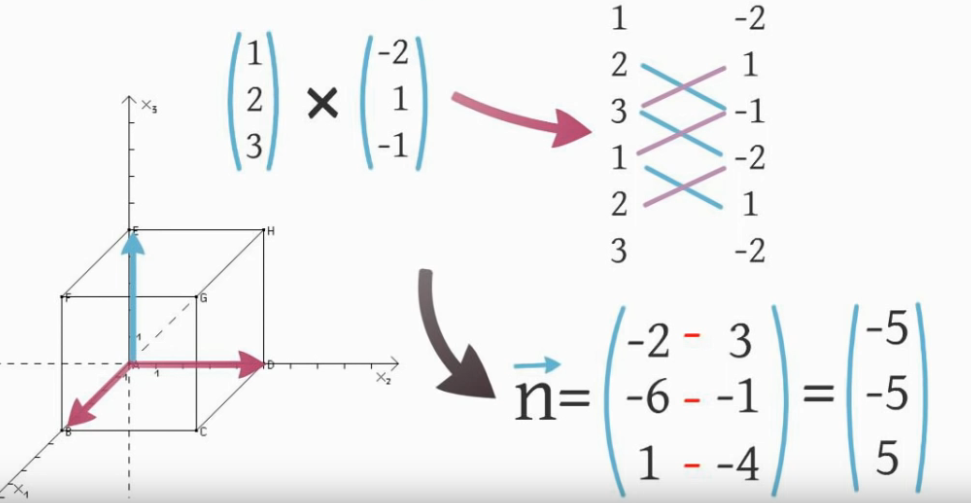
Cross product
Das Kreuzprodukt zweier Vektoren im 3D-Raum ergibt einen Vektor, der senkrecht (orthogonal) auf beiden Eingangsvektoren steht.
Lage von Geraden im Raum
(Stützvektor) Welche Koordinaten schneidet eine Gerade?
Gegenseitige Lage von Geraden im Raum
Berechnen ob sie
- Parallel
- gleich
- sich schneidend
- windschief
sind.
Normalformen und Projektion
Links
Ganze Youtube Playlist https://www.youtube.com/playlist?list=PLjaA00udJtOpn73fqft-kcdST4ac2HW4U
Matritzen: http://www.opengl-tutorial.org/beginners-tutorials/tutorial-3-matrices/
Vektorrechnen https://www.youtube.com/watch?v=fjOdtSu4Lm4